 |
Smart Minotaur
|
 |
Smart Minotaur
|
Der im Projekt verwendete Roboter stellt für die Odometrie Motoren zur Verfügung. Diese bieten jedoch eine sehr geringe Genauigkeit und Zuverlässigkeit. Zusätzlich kann sich dies, je nach Fahrfläche verschlechtern (Räder drehen durch). Um die Odometrie zu verbessern, werden im Smart-Minotaur Projekt zusätzlich Maussensoren von herkömmlichen Gaming-Computermäusen verwendet. Diese messen die zurückgelegte X- und Y-Distanz, indem die mithilfe von Lasern erzeugten Bilder der Oberfläche verarbeitet werden. Die in diesem Projekt verwendeten Sensoren sind vom Typ Philips PLN2033 twin-eye Laser. Diese verfügen über eine sehr hohe Präzision (bis zu 6400 CPI - Counts Per Inch) beim Messen der zurückgelegten X- und Y-Distanzen.
In diesem Abschnitt werden die wichtigsten Funktionen des PLN2033 Sensors erläutert. Weitere Informationen befinden sich im Datenblatt.

Der PLN2033 besitzt verschiedene 16-Bit Register mit welchen dieser konfiguriert und gesteuert werden kann. Es werden zwei Laser verwendet, um die X- und Y-Positionsänderungen zu messen. Mithilfe dieser Laser werden Bilder der Oberfläche erstellt. Intern verarbeitet ein DSP (digital signal processor) diese Bilder und bestimmt aus diesen den zurückgelegten Weg. Die Auflösung kann von 100 bis 6400 CPI eingestellt werden. CPI (counts per inch) bestimmt, wie oft der Sensor pro Inch (2.54cm) die internen Zähler erhöht. Daher bestimmen die CPI-Einstellung die Auflösung des Sensors. Die Ansteuerung des Sensors erfolgt über SPI und kann mit bis zu 8Mhz (Linux SPI Treiber Clock) betrieben werden. Der PLN2033 benötigt zum Arbeiten 3.3V.
Beim Abfragen der Sensor Displacement-Werte werden die Werte der internen X- und Y-Zähler zurückgegeben. Im folgenden Bild werden diese Register zwei mal (blauer Kasten) ausgelesen. Delta X/Y stellen dabei den zurückgelegten Weg in X- und Y-Richtung dar.
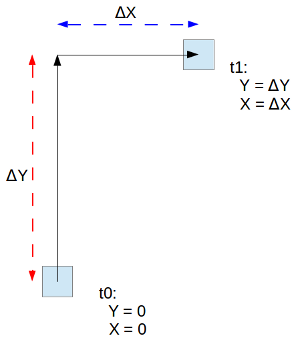
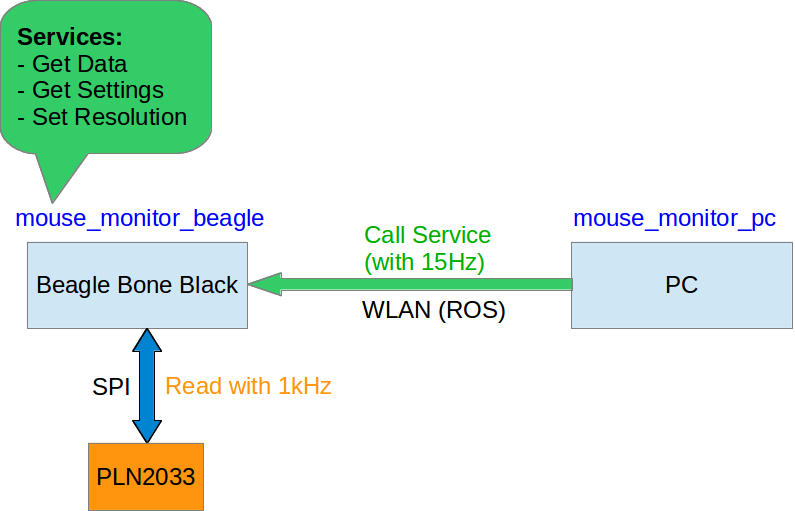
Das Beagle Bone Black (BBB) besitzt zwei SPI Ports. SPI1 wird verwendet, da zwei PLN2033 Sensoren angeschlossen werden und dieser im Gegensatz zu SPI0 zwei Chip-Selects besitzt.


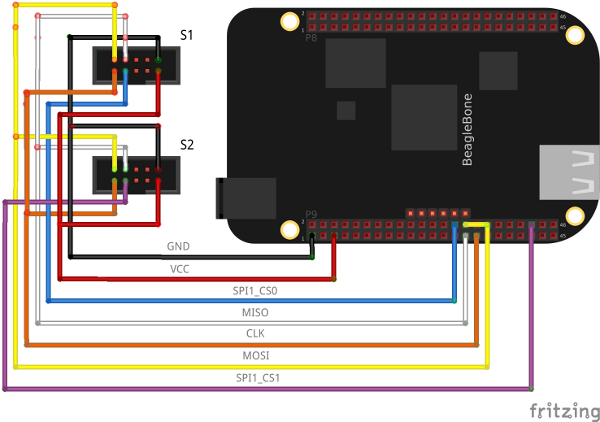
Zum Ansteuern des PLN2033 wird der SPI-Bus verwendet. Für das Smart-Minotaur Projekt wurden zwei Sensoren an den Roboter montiert (Nur einer wird benötigt, um Position und Ausrichtung zu bestimmen). Da zum Ansteuern von zwei Slaves auf dem SPI Bus zwei Chip-Selects benötigt werden, wird der SPI1 Port des Beagle Bones verwendet. Um Daten zu Senden und Empfangen wird der Linux spidev Treiber verwendet, welcher rudimentäre Funktionen anbietet. Um den SPI1 Port benutzen zu können, muss dieser erst im Device Tree registriert werden. Dafür wird ein Device- Tree-Source-File benötigt (dts), welche die korrekten Pins, Register und Funktionalitäten des SPI Gerätes spezifiziert. Diese Datei wird kompiliert und im Linux Kernel aktiviert. Wichtig ist, das HDMI des BBB auszuschalten, da dieses auch SPI1 Ports verwendet und die Kommunikation stören würde. Nach erfolgreicher Aktivierung kann auf die Slaves über Gerätedateien zugegriffen werden:
/dev/spidev1.0 CS0 /dev/spidev1.1 CS1
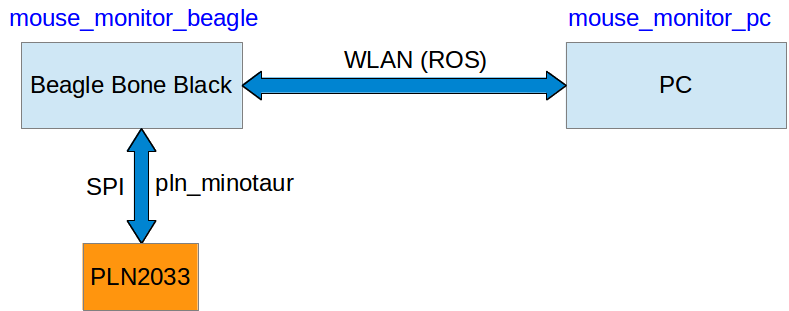
Die Mouse Monitor Software wird zum Testen, Debuggen und Überprüfen der Maussensoren verwendet. Die Anwendung verfügt über eine Vielzahl von Funktionen. Sie besteht aus zwei Teilen:
Zur Kommunikation wird das ROS Message System verwendet. Daher sind beide Teile als ROS Packages realisiert. Entwickelt wurden beide Teile in C++. Zur Darstellung der Daten auf dem PC wird Qt verwendet. Die pln_minotaur Bibliothek wird zum Ansteuern der Sensoren benutzt.
Eine genaue Beschreibung der pln_minotaur Bibliothek befindet sich auf folgender Seite: pln_minotaur
Die x86 Version der pln_minotaur Bibliothek muss beim Kompilieren des mm_p Package dazu gelinkt werden, da daraus Datenstrukturen verwendet werden. Zum Erstellen beider Teile kann das mitgelieferte compile-script verwendet werden. Da das cross-kompilieren von ROS nicht unterstützt wird, muss der BBB Teil direkt auf dem BBB kompiliert werden.
# Auf PC: Mouse Monitor PC ./compile mm_p # Auf BBB: Mouse Monitor Beagle ./compile mm_b
Die PC Node empfängt die Sensordaten, verarbeitet diese und stellt sie grafisch dar. Über diese Anwendung kann die CPI Auflösung der Sensoren eingestellt werden. Zusätzlich kann eine variable Sample Rate der GUI konfiguriert werden (meist 15-100Hz). Im folgenden werden einige Features der Anwendung erklärt.
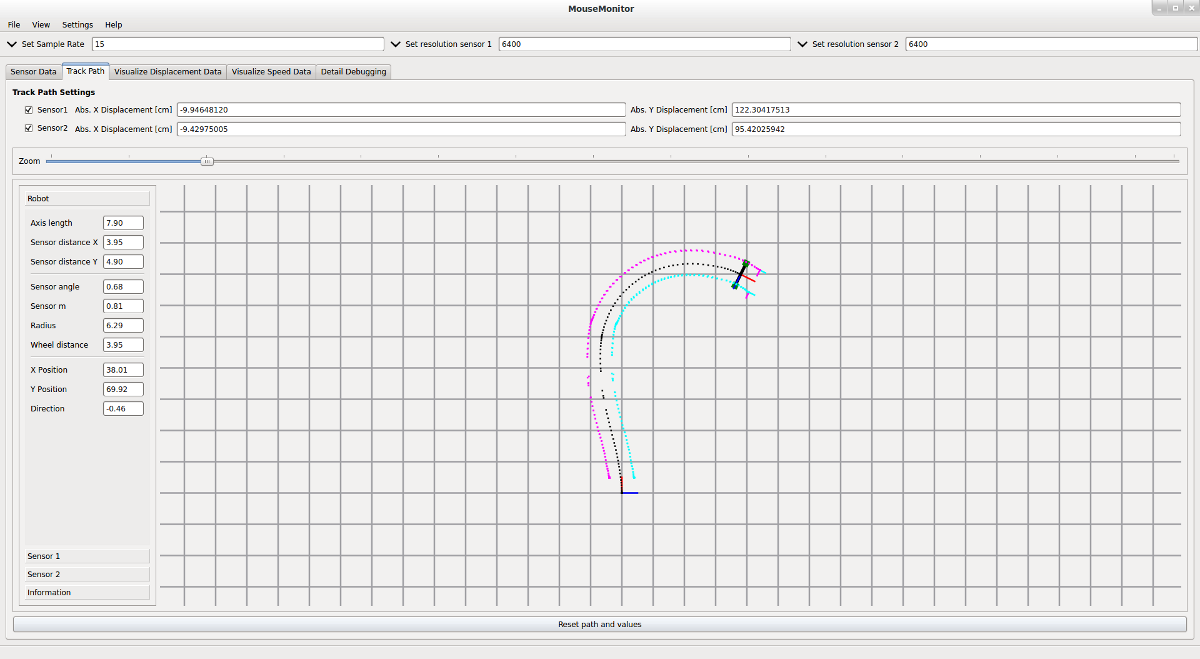
Features:
Folgendes Bild zeigt die Y- und X-Displacement Werte der zwei Sensoren bei einer Geradeausfahrt. Dabei ändern sich die X-Werte nur minimal. Die Ausreißer bei den Y-Werten entstehen aufgrund der WLAN Latenz, welche aber keine negativen Auswirkungen auf die Funktionalität hat.
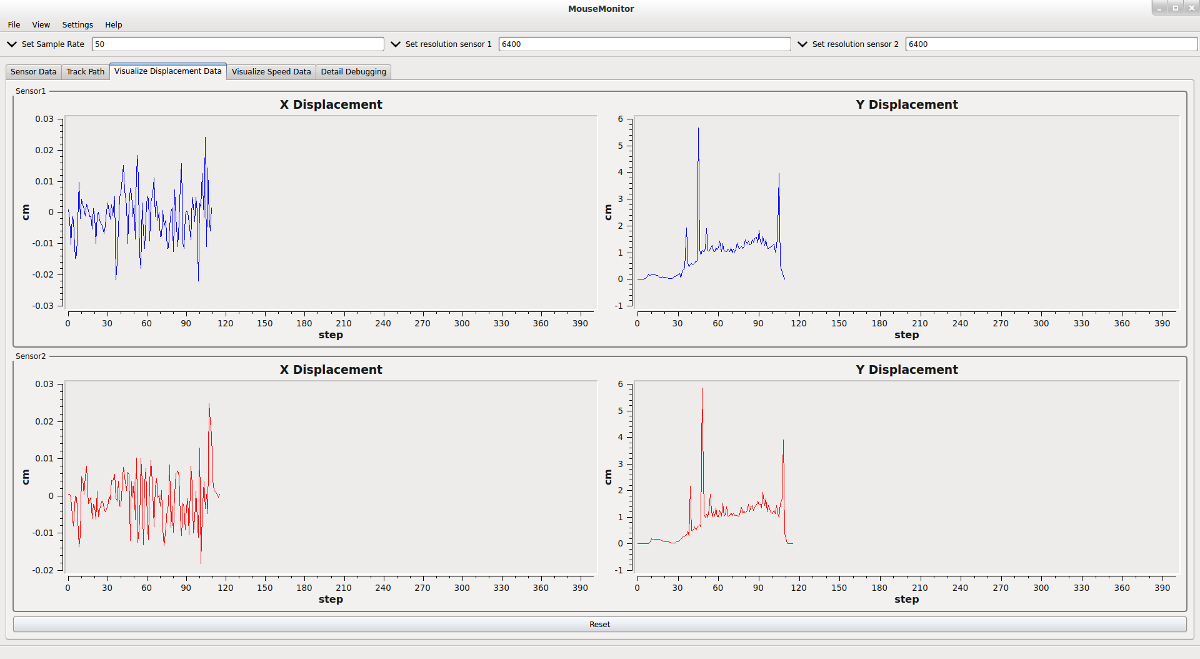
Diese Anwendung ist für das Auslesen der Maussensor Displacement und Speed Daten zuständig und verwendet dafür die pln_minotaur Bibliothek. Daten werden mit einer 1kHz Frequenz ausgelesen und aufsummiert. Auf Anfrage der PC Node sendet die Applikation die gesammelten Daten zur PC Node. Zusätzlich bietet diese Funktionen an, um von der PC Node die Auflösung (CPI) der Sensoren zu setzen, sowie zum Abfragen des Status der Sensoren.
Für die WLAN Kommunikation zwischen Beagle Bone und PC existiert jeweils eine ROS Node. Dabei werden ROS Services verwendet. Mouse Monitor PC kann in konfigurierbaren Intervallen die Sensordaten abfragen.
Beim Abfragen der Sensordaten schickt die Beagle Bone Node folgende ROS Message:
// MouseMonitorSensorData.msg string id float64 x_disp float64 y_disp float64 x_speed float64 y_speed
Zusätzlich existieren Messages/Services zum Setzen der Sensor Auflösung, sowie zum Abfragen der Sensorkonfiguration.
// MouseMonitorSensorSettings.msg string spiDevice uint16 status_register uint16 delta_x_disp_register uint16 delta_y_disp_register uint16 command_high_register uint16 command_low_register uint16 memory_pointer_register uint16 memory_data_register uint16 mode_control_register uint16 power_control_register uint16 mode_status_register uint16 system_control_register uint16 miscellaneous_register uint16 interrupt_output_register
Die Sensor Displacement-Werte werden mit einer konfigurierbaren sample rate (zum Beispiel 15Hz) vom PC-Teil abgefragt. Pro Anfrage schickt die BBB Node die intern mit 1kHz aufsummierten Werte zurück.
Bei der Berechnung der Position und der Ausrichtung des Roboters wird eine korrekte Montierung der Maussensoren vorausgesetzt. Um exakte Berechnungen durchführen zu können, müssen die Sensoren richtig in Fahrtrichtung ausgerichtet sein. Das bedeutet, dass sich bei einer Vorwärtsbewegung nur die Y-Werte ändern. Da eine korrekte Montierung sehr schwierig ist (und das durch das Lego ohnehin unmöglich ist) müssen die Sensoren kalibriert werden um den Fehler der schrägen Montierung auszugleichen.
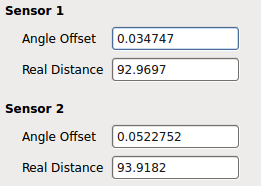
Über die GUI kann ein Kalibrierungswizard gestartet werden. Beim Kalibrieren wird die Gesamtdistanz einer gefahrenen Geradeausfahrt gemessen und der Winkel gegenüber der idealen Geradeausfahrt bestimmt. Alle folgenden Messdaten (Vektoren) werden mithilfe einer 2D Rotationsmatrix um diesen Winkel gedreht.
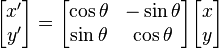
Folgendes Bild zeigt eine Geradeausfahrt ohne Kalibrierung. Es ist deutlich der Drift des Roboters zu erkennen.
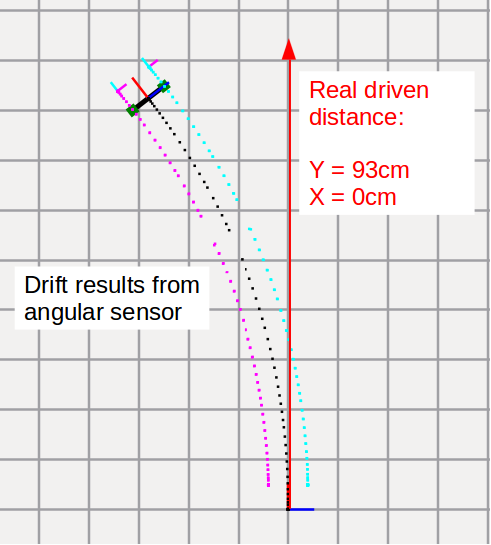
Beim Kalibrieren wird der Winkel gegenüber der idealen Geradeausfahrt bestimmt. Zu beachten ist hierbei, dass der Korrektur-Winkel anhand der rohen Messdaten berechnet wird, nicht aus den verarbeiteten (Roboter Position und Ausrichtung) wie im Bild dargestellt.
Nach einer Geradeausfahrt wird der Winkels zwischen idealer Geradeausfahrt (X-Anteil = 0) und gemessener Geradeausfahrt (X-Anteil != 0 wegen schräger Montierung) bestimmt:
if (s1YDisplacement > 0)
atanRealDistance = M_PI/2;
else if (s1YDisplacement < 0)
atanRealDistance = -M_PI/2;
s1AngleOffset = atanRealDistance - std::atan2(s1YDisplacement, s1XDisplacement);
Anschließend kann die Rotationsmatrix für alle empfangenen Messwerte angewendet werden:
double angle = calibrationData.getS1AngleOffset(); // Rotationmatrix data.x_disp = (std::cos(angle) * data.x_disp) + (-std::sin(angle) * data.y_disp); data.y_disp = (std::sin(angle) * data.x_disp) + (std::cos(angle) * data.y_disp);
Die Berechnung der Roboterposition sowie Ausrichtung wird in diesem Abschnitt beschrieben. Dabei werden nicht wie ursprünglich angenommen zwei Sensoren benötigt, sondern lediglich ein Sensor. Im folgenden werden zwei Lösungsansätze vorgestellt.
Das Bestimmen der Roboterposition aufgrund der rohen Sensor X- und Y-Displacement Daten ist nicht trivial. Es ist nicht möglich die reinen Sensordaten mit der aktuellen Position des Roboters/Sensors zu addieren. Da bei einer Rotation des Roboters auch das Koordinatensystem (die Ausrichtung) des Sensors rotiert, ergeben die gemessenen Werte nicht die benötigten Delta X und Y, sondern einen Vektor der erst auf einen Steuervektor mit Geschwindigkeit und Winkelgeschwindigkeit umgerechnet werden muss. Lediglich die Y-Werte könnten bei einer reinen Geradeausfahrt (ICS im unendlichen) addiert werden (unter Berücksichtigung der aktuellen Ausrichtung), da der Sensor mit der Y-Achse in Roboterausrichtung montiert ist. Rotiert sich der Roboter gleichzeitig, müssen die oben genannten Probleme berücksichtigt werden.
Mit der Annahme, dass der Sensor kalibriert wurde kann von folgender Situation ausgegangen werden.
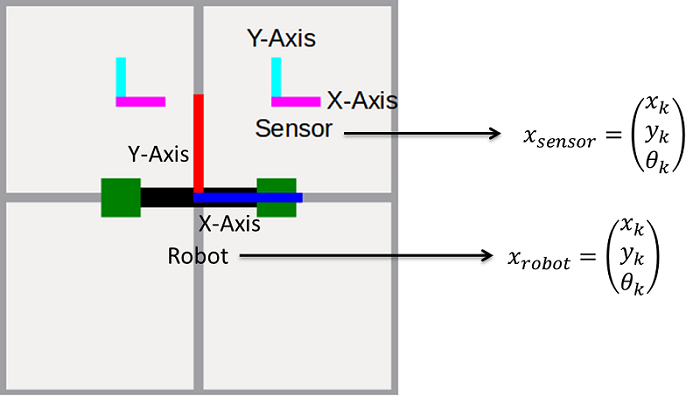
Folgende Koordinatensysteme sind dargestellt:
Roboter und Sensor speichern jeweils Position und Ausrichtung als Vektoren \(x_{robot}\) und \(x_{sensor}\).
Obwohl im Bild zwei Sensoren dargestellt sind, wird bei den Berechnungen nur der rechte Sensor verwendet. Bei einer Geradeausfahrt ändert sich nur die Y-Koordinate. Bei einer Rotation ändern sich aufgrund der verschobenen Position des Sensors X- sowie Y-Koordinaten.
Zusätzlich sind folgende Parameter des Roboters bekannt, welche durch Ausmessen bestimmt wurden.
double axisLength; // cm double distanceToSensor_x; // cm double distanceToSensor_y; // cm double distanceToSensor_radius; // cm double distanceToWheel; // cm double sensorAngle; // Radians double m;
Die folgenden Abschnitte beschreiben, wie aus den Sensordaten der Steuervektor \(u_k\) mit Geschwindigkeit ( \(v\)) sowie die Winkelgeschwindigkeit ( \(\omega\)) des Roboters bestimmt wird. Ist der Steuervektor bekannt kann die Position sowie Ausrichtung des Roboters mithilfe der Koppelnavigation bestimmt werden.
Im nächsten Abschnitt wird von einer einfacheren Montierung des Sensors ausgegangen um die Herleitung zu verdeutlichten. Anschließend wird die flexiblere und allgemeinere Lösung besprochen, welche eine variable Montierung des Sensor erlaubt.
Ist der Sensor in einer rechtwinkligen Position zur Tangente des Kreises den der Sensor um die Achse des Roboters bildet montiert, vereinfacht sich die Berechnung sehr.
Bei einer reinen Rotation ändern sich lediglich die X-Werte des Sensors. Der Sensor bewegt sich nur auf dem Kreis den er mit den Roboter bildet - der Radius bleibt immer gleich. Der Y-Anteil ist 0. Bei einer Geradeausfahrt (Vorwärts oder Rückwärts) ändern sich nur die Y-Werte. Der X-Anteil ist 0. Geradeausfahrt und Rotation können daher einfach unterschieden werden.
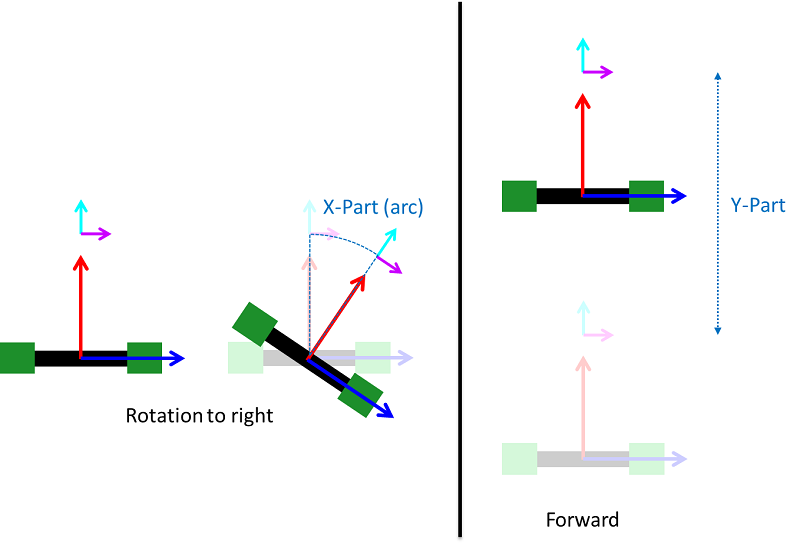
Der zu den Sensorwerten gehörende Steuervektor bei Geradeausfahrt und Rotation kann einfach bestimmt werden. Die gemessene X-Strecke (in Abbildung 'X-Part') kann direkt über die Kreisbogenformel in den Rotationswinkel ( \(\Delta\beta\)) umgerechnet werden. Da in jedem Messabschnitt von einer konstanten Geschwindigkeit ausgegangen wird, wird der Betrag der Winkelgeschwindigkeit ( \(\omega\)) bestimmt indem der Quotient aus Rotationswinkel und der dafür benötigten Zeit berechnet wird.
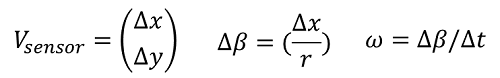
Die gemessene Y-Strecke (in Abbildung 'Y-Part') wird ebenfalls durch \(\Delta t\) geteilt.
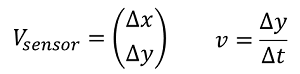
Folgender Steuervektor ergibt sich:
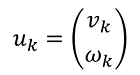
Im oben Beschriebenen Ansatz muss der Sensor immer mit Y-Achse in Richtung Radius montiert werden. Da das nicht sehr flexibel ist wird nun ein Ansatz vorgestellt der eine variable Montierung des Sensors erlaubt. Dabei ist der Sensor wie im folgenden Bild verschoben, zeigt aber immer noch mit der Y-Achse in die gleiche Richtung wie der Roboter.
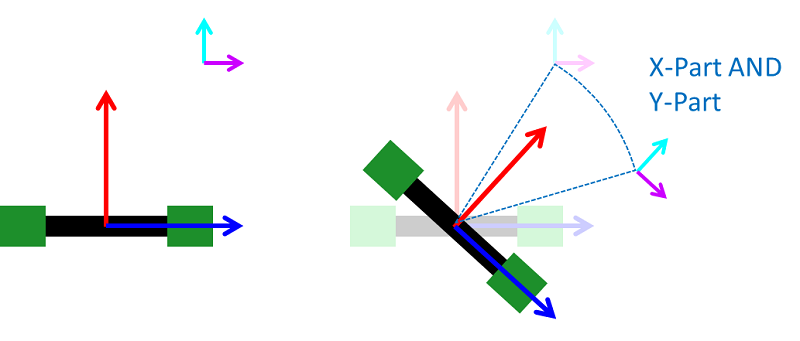
Da die Sensoren nicht im rechten Winkel mit der Kreistangente montiert sind, ändern sich bei einer reinen Drehung des Roboters X- sowie Y-Koordinaten des Sensors in einem linearen Verhältnis. Bei einer Geradeausfahrt ändern sich immer noch wie bei der einfachen Montierung nur die Y-Koordinaten.
Um anhand der Sensor-Displacement Daten die Position des Roboters zu bestimmen, muss aus diesen Daten (Delta X, Delta Y) die jeweilige zurückgelegte Distanz bei einer Drehung sowie bei einer Geradeausfahrt bestimmt werden. Die Werte müssen in Drehung und Geradeausfahrt unterteilt werden, da bei gleichzeitiger Rotation und Geradeausfahrt diese nicht unterschieden werden können. Es muss bekannt sein welche Werte auf einen Rotationswinkel umgerechnet werden müssen und welche Werte für die Bewegung in positiver oder negativer Y-Richtung (Geradeausfahrt) verwendet werden.
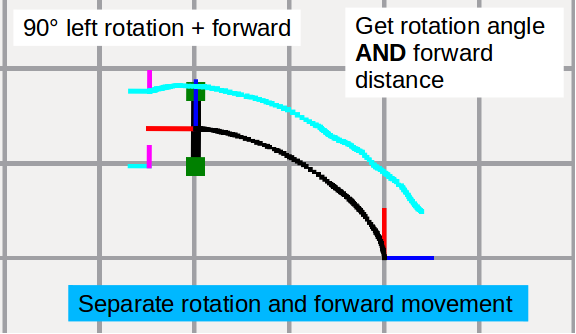
Bekannt: Eingangsvektor des Sensors
\(V_{sensor} = (\Delta x, \Delta y)\)
Kann unterteilt werden in:
Gesucht: Neue Position und Ausrichtung des Sensors
Folgende Abbildung zeigt den Eingangsvektor ( \(V_{sensor}\)) sowie die benötigten Vektoren \(V_r\) und \(V_f\).
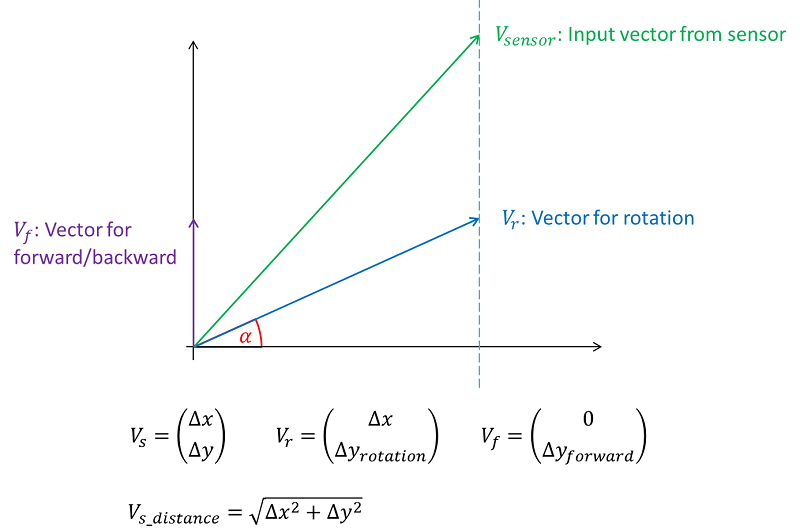
Sind die Vektoren \(V_r\) und \(V_f\) welche die zurückgelegte Distanz bei Rotation oder Geradeausfahrt darstellen bekannt, kann aus diesen der benötigte Steuervektor berechnet werden. Um diesen Vektor zu berechnen wird das Verhältnis der Änderung der X- und Y-Koordinaten bei einer Drehung aus den empfangenen Sensorwerten herausgerechnet. Das Verhältnis von X- und Y-Werten bei einer Drehung ist bekannt. Es entspricht genau dem im folgenden Bild dargestellten Winkel (alpha).
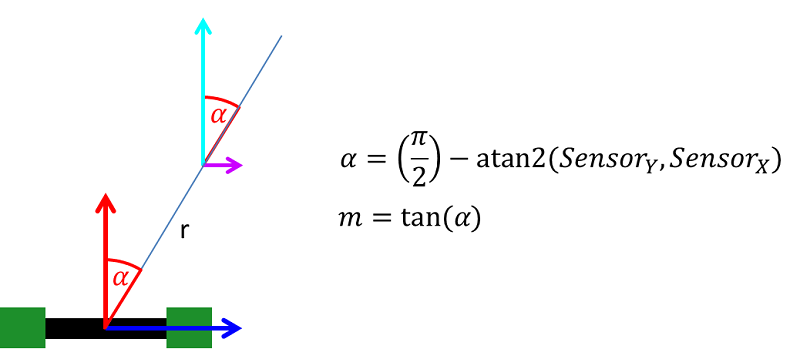
Da die Maße des Roboters bekannt sind kann dieser Winkel sowie die Steigung bestimmt werden. Dabei muss lediglich der Winkel der Y-Achse des Sensors gegenüber dem Radius bestimmt werden. Mit diesem Wissen kann der Y-Anteil bei einer Drehung bestimmt werden. Es ist bekannt, dass sich bei Geradeausfahrt nur die Y-Werte des Sensors ändern. Der X-Anteil des Eingansvektors \(V_s\) ist Bestandteil der Rotation. Da die Steigung sowie der X-Anteil von \(V_r\) bekannt sind, kann dessen Y-Anteil berechnet werden. Mithilfe des Satz des Pythagoras wird die zurückgelegte Distanz bei Drehung sowie Geradeausfahrt berechnet. Die gesamte zurückgelegte Distanz minus die Kurvendistanz ergibt die zurückgelegte Strecke bei Geradeausfahrt (bzw. Rückwärtsfahrt).
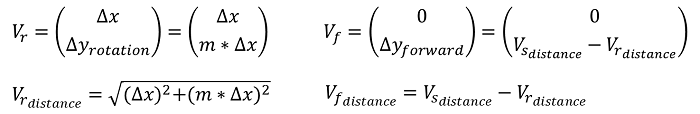
Da die zurückgelegte Distanz bei einer Drehung bekannt ist, kann mithilfe der Kreisbogenformel der Drehwinkel bestimmt werden. Der Quotient aus Drehwinkel und benötigter Zeit ergibt \(\omega\).
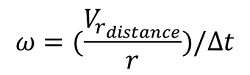
\(v\) wird aus \(V_{fdistance}\) berechnet.
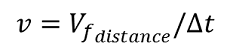
Zusammengefasst ergeben sich folgende Formeln zur Berechnung des Steuervektors:
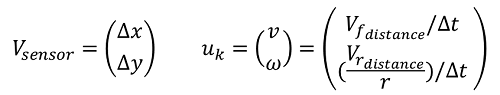
Ein weiterer Ansatz zur Berechnung des Steuervektors ist über die allgemeinen Regeln der Kinematik. Folgende Formel beschreibt den Zusammenhang von Position sowie Geschwindigkeit zweier starrer Körper um \(v\) und \(\omega\) zu bestimmen.
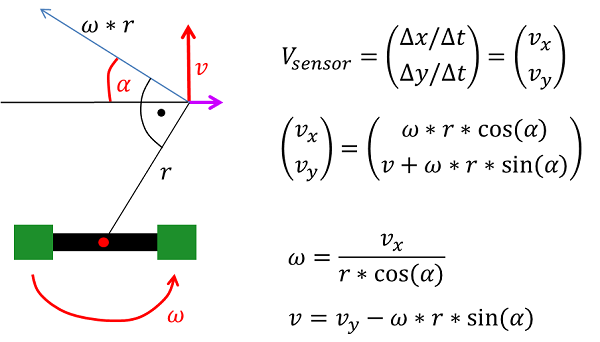
Hierbei beschreibt \(\omega * r\) den Geschwindigkeitsvektor der Rotation.
Um die Odometrie weiterhin zu verbessern, kann zusätzlich ein zweiter Sensor verwendet werden. Das Einbeziehen der zwei Räder zur Berechnung der Odometrie verbessert diese weiter.
Die Berechnung wird bisher zu Debuggingzwecken auf einem PC ausgeführt. Die wichtigsten Klassen befinden sich in der Datei Robot.h. Roboter und Sensoren werden als Objekte der Superklasse Object erzeugt, welche als Hauptfunktion die Methoden forward() sowie rotate() zum Bewegen der Objekte bietet. Implementiert wurde der im vorherigen Abschnitt beschriebene Ansatz 1.
Robot:
Sensor:
Zusätzlich wird bei allen Objekten der zurückgelegte Pfad im globalen Koordinatensystem abgespeichert.
Die Methode move() des Roboters wird verwendet um den Roboter aufgrund der X- und Y-Displacement Werte eines Sensors zu bewegen. Dabei werden die oben erklärten Berechnungen ausgeführt, welche als Ergebnis den Drehwinkel sowie die zurückgelegte Distanz bei Geradeausfahrt liefern. Je nach Richtung werden die forward() und rotate() Methoden ausgeführt.
Der folgende Code-Ausschnitt zeigt die Implementierung der move() Funktion.
// V_r = Vector for rotation
// V_f = Vector for forward/backward
// V_rd = Vector for rotation and forward/backward
double Vx_r = dX;
double Vy_r = dX * attributes.m;
double Vdist_r = sqrt(pow(Vx_r, 2) + pow(Vy_r, 2));
double Vm_r = Vy_r/Vx_r;
double Vangle_r = atan(Vm_r);
// From circular arc (Vdist_r)
double rotateAngle = Vdist_r / attributes.distanceToSensor_radius;
// Rotation direction
if (dX >= 0)
rotate(rotateAngle);
else
rotate(rotateAngle * -1);
double Vdist_rf = sqrt(pow(dX, 2) + pow(dY, 2));
double Vdist_f = Vdist_rf - Vdist_r;
// Forward or backward
if (dY < 0)
Vdist_f *= -1;
forward(Vdist_f);
Während der Durchführung des Projektes traten einige Probleme bezüglich der PLN2033 Sensoren auf. Diese werden in diesem Abschnitt erläutert.
Aufgrund der schlechten Testumgebung und schlechtem Hardware-Aufbau war die Fehlersuche sowie Validierung der Sensor-Funktionalität sehr schwierig. Der PLN2033 ist ein hoch-präziser Lasersensor. Um korrekte Aussagen über seine Funktionsweise zu machen, ist ein professioneller Prüfstand erforderlich welcher in diesem Projekt nicht vorhanden war. Die Tests mussten per Hand (Lego-Wagen per Hand schieben, drehen etc.) durchgeführt werden, was genaues Messen unmöglich machte. Eine exakte Geradeausfahrt, Drehung, etc. konnte damit nicht erreicht werden.
Zum Testen sowie bei der Endmontierung auf dem Roboter wird Lego benutzt, was wiederum einige Probleme mit sich führt:

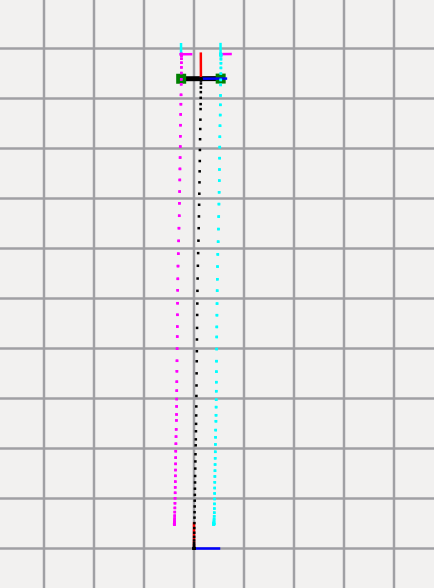
Das folgende Bild zeigt eine Rundfahrt des Roboters. Trotz Kalibrierung erkennt die Software einen minimalen Drift - der Roboter stoppt nicht exakt an der Ausgangsposition.
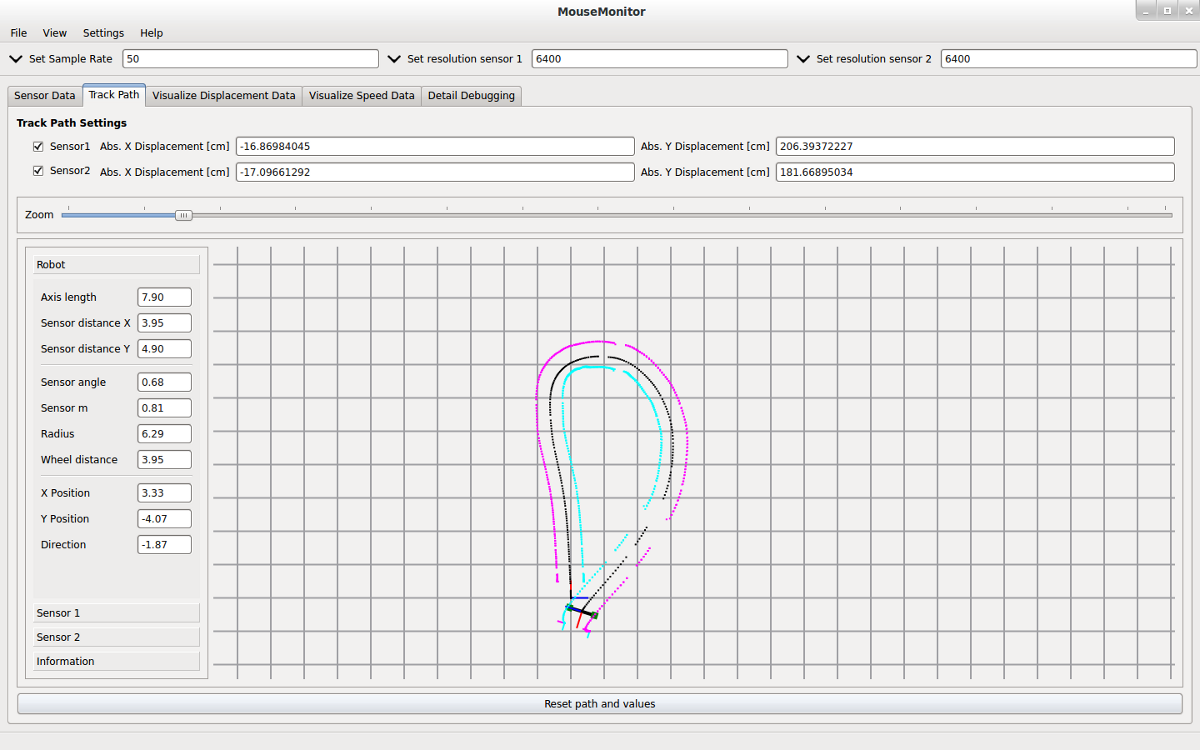
Zum Testen der Grundfunktionalität der Sensoren wurde folgender Test auf dem Beagle Bone ausgeführt:
Teststart
Reset der internen Register.
Testdurchführung
Der Roboter wird eine festgelegte Strecke (10cm) per Hand vorwärts bewegt. Dabei zählen die internen X- und Y-Register hoch. Es wurde mit einer festgelegten Auflösung sichergestellt, dass kein Überlauf bei der 10cm Strecke auftreten kann.
Testende
Die Register Werte des Sensors werden ausgelesen. Nun sollten die Y-Werte (geradeaus) immer 10cm betragen.
Beobachtung
Bei mehreren Test wurde festgestellt das bei einigen Testfahrten die Y-Werte sehr kleine Werte annehmen. Dies passierte ungefähr in 10%-20% der Fälle.
Nach langem Debuggen wurde erkannt, dass die Sensoren sehr empfindlich auf anheben reagieren. Da bei Bewegungen von Hand die Sensoren sehr wackeln, wurde beim Anhalten des Roboters (nach 10cm) in einigen Fällen das Lift-Bit des Sensors gesetzt. Dieses Lift-Bit wird gesetzt, wenn der Sensor zu weit von seiner kalibrierten Höhe angehoben wird. Passiert dies, werden alle internen Zähler zurückgesetzt und die Werte sind verloren.
Eine Lösung für dieses Problem ist es, die Sensorwerte mit einer sehr hohen Abtastrate (1kHz) abzufragen, um den Fehler sehr gering zu halten. Zusätzlich können bei Aktivierung des Lift-Bits interpolierte Werte als Ersatz in die Messdaten integriert werden.
Ursprünglich wurden die Messdaten mit einer sehr geringen Frequenz abgefragt. Dadurch entstand der oben genannte Fehler. Um diese kleinen Messwerte herauszufiltern wurde ein Median-Filter auf der PC-Seite eingesetzt. Allerdings verschlechtert dieser die Messergebnisse. Da die Kommunikation über WLAN erfolgt, entstehen Latenzen bei der Übertragung der Messdaten. Bei der Abfrage der Messdaten wird erst auf eine Antwort der aktuellen Anfrage an das BBB gewartet. Erst wenn diese eingetroffen sind wird nach dem nächsten Paket gefragt. Die übertragenen Daten bleiben zwar korrekt, allerdings kann die Übertragung von Paketen länger dauern. Dadurch hat der Sensor mehr Zeit Messdaten zu sammeln. Langsamere Pakete enthalten dadurch höhere Displacement-Werte. Da der Median diese als Ausreißer ausfiltert obwohl diese korrekt sind, verschlechtert dieser die Messergebnisse.
Durch das Speichern der Messwerte mit einer hohen Sample-Rate auf dem BBB entsteht dieser Fehler nicht mehr.
Das Konfigurieren des Device Trees für SPI1 mit zwei Chip-Selects unter Ubuntu brachte einige Probleme mit sich. Das Device Tree File musste mit den richtigen Pins erweitert werden. Zusätzlich musste HDMI deaktiviert werden.
Mit einer hohen Sample Rate ist der Lift-Bit Fehler sehr gering. Mit einem geeignetem Filter könnte der Fehler noch weiter verringert werden. Bei 1kHz kann dieser vernachlässigt werden. Zusätzlich könnten anstatt dem Aufsummieren der Daten auf dem BBB diese auch als Schritte abgespeichert werden. Allerdings reichen die Abfrage-Intervalle der GUI vollkommen aus um schnelle Kurven zu erkennen. Auch die WLAN Latenzen stören das Messergebnis nicht. Der Sensor hat eine Varianz von 1-2cm auf 100cm. Unabhängig davon driften die gemessenen Werte ab ca. 1m etwas ab. Dies passiert aufgrund der Lego-Montierung welche sich immer wieder verschiebt. Trotz kalibrieren sind die Messwerte nicht optimal. Nur ein Sensor wird zum Bestimmen der Position und Ausrichtung benötigt.
